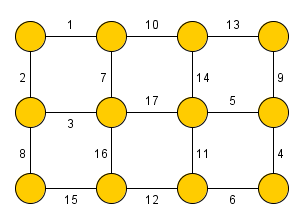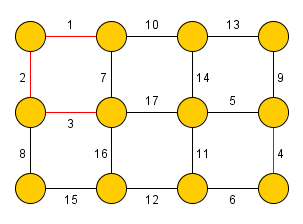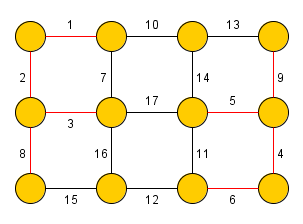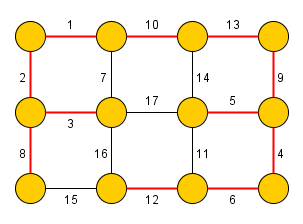
Kruskal's algorithm is used to find the minimum/maximum spanning tree in an undirected graph (a spanning tree, in which is the sum of its edges weights minimal/maximal). The algorithm was devised by Joseph Kruskal in 1956.
Description
At first Kruskal's algorithm sorts all edges of the graph by their weight in ascending order. Than the procedure iteratively adds the edges to the spanning tree in such a way, that no cycle may occur (the procedure terminates after adding edges).
To ensure that there is no cycle in the graph, the procedure stores for each vertex its membership to a connected component using a disjoint-set data structure. The disjoint set offers two operations: union (merges two connected components) and find (determines connected component membership of the given node).
Complexity analysis
The asymptotic complexity of the algorithm is , provided a comparison based algorithm is used to sort the edges. If we use a linear time sorting algorithm (e.g. counting sort) or the edges are already presorted, than the complexity of Kruskal's algorithm is
, where
is the inverse Ackermann function (corresponds with the time complexity of union and find operations).
Code
/**
* Kruskal's algorithm
* @param graph graph
* @param w weight vector of the edges
* @return minimum spanning tree
*/
SpanningTree kruskalAlgorithm(Graph graph, weights w)
SpanningTree tree
for Node n : graph do
makeSet(n) //every edge is considered as a separate component
List edges = sort(graph.getEdges(), w) //order the edges according to their weight in ascending order
for Edge e in edges do
if findSet(e.start) != findSet(e.end) //if the source and target are in different components, than we are not creating a cycle
tree.add(e) //add the edge to the spanning tree
union(e.start, e.end) //merge the connected components
if tree.edgeCount() == graph.nodeCount() - 1 //if the spanning tree is complete
break //terminate the algorithm
return tree
/**
* Kruskal's algorithm
* @author Pavel Micka
*/
public class KruskalAlgorithm {
/**
* Finds the minimum spanning tree of the given grapg with n vertices (the vertices are numbered
* 0, 1, ..., n-1)
* @param edges edges of the undirected graph
* @param nodeCount number of vertices (n)
* @return minimum spanning tree
*/
public static List<Edge> kruskalAlgorithm(List<Edge> edges, int nodeCount) {
DisjointSet ds = new DisjointSet(nodeCount);
List<Edge> spanningTree = new ArrayList<Edge>();
Collections.sort(edges);
int i = 0;
while (i != edges.size() && spanningTree.size() != nodeCount - 1) {
Edge e = edges.get(i);
if(ds.find(e.getFrom()) != ds.find(e.getTo())){
spanningTree.add(e);
ds.union(e.getFrom(), e.getTo());
}
i++;
}
return spanningTree;
}
}
// ***************************** //
// * Data Structures * //
// ***************************** //
/**
* Edge of a undirected graph
* @author Pavel Micka
*/
class Edge implements Comparable<Edge> {
private int from; //from
private int to; //to
private int weight; //weight
public Edge(int from, int to, int weight) {
this.from = from;
this.to = to;
this.weight = weight;
}
/**
* Compare to function (greater weight => is greater than)
* @param o
* @return
*/
public int compareTo(Edge o) {
if (this.getWeight() > o.getWeight()) {
return 1;
} else if (this.getWeight() < o.getWeight()) {
return -1;
} else {
return 0;
}
}
/**
* @return the from
*/
public int getFrom() {
return from;
}
/**
* @param from the from to set
*/
public void setFrom(int from) {
this.from = from;
}
/**
* @return the to
*/
public int getTo() {
return to;
}
/**
* @param to the to to set
*/
public void setTo(int to) {
this.to = to;
}
/**
* @return the weight
*/
public int getWeight() {
return weight;
}
/**
* @param weight the weight to set
*/
public void setWeight(int weight) {
this.weight = weight;
}
}
/**
* Implementation of the disjoint set structure
* @author Pavel Micka
*/
class DisjointSet {
private Node[] nodes;
public DisjointSet(int nodeCount) {
nodes = new Node[nodeCount];
for (int i = 0; i < nodeCount; i++) {
nodes[i] = new Node();
nodes[i].id = i;
}
}
/**
* Unions sets, which contain vertices "a" and "b"
* Union is always performed as merging "B" into "A"
* @param a number of a node "a"
* @param b number of a node "b"
* @return number of a representative of the merged component
*/
public int union(int a, int b) {
Node repA = nodes[find(a)];
Node repB = nodes[find(b)];
repB.parent = repA;
return repA.id;
}
/**
* Returns representative of the compoment which contains the given node
* @param a number of a node, whose representative we are looking for
* @return number of the representative
*/
public int find(int a) {
Node n = nodes[a];
int jumps = 0;
while (n.parent != null) {
n = n.parent;
jumps++;
}
if (jumps > 1) repair(a, n.id);
return n.id;
}
/**
* Performs compression of the path
* @param a
* @param rootId
*/
private void repair(int a, int rootId) {
Node curr = nodes[a];
while (curr.id != rootId) {
Node tmp = curr.parent;
curr.parent = nodes[rootId];
curr = tmp;
}
}
@Override
public String toString() {
StringBuilder builder = new StringBuilder();
for (int i = 0; i < nodes.length; i++) {
builder.append(find(i) + " ");
}
return builder.toString();
}
/**
* Vertex of an n-ary tree
*/
private static class Node {
/**
* Parent
*/
Node parent;
/**
* Node id
*/
int id;
}
}
Sources
- KOLÁŘ, Josef. Teoretická informatika. 2. edition. Praha : Česká informatická společnost, 2004. 205 p. ISBN 80-900853-8-5.