Jarník-Prim algorithm

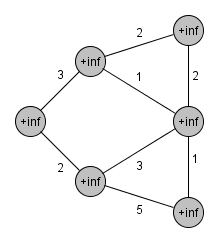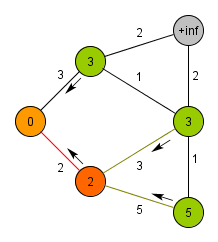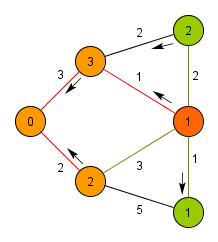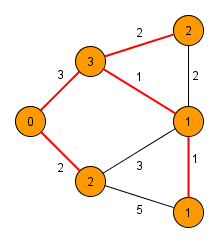
The Jarník-Prim algorithm (Jarník's algorithm, Prim's algorithm, DJP algorithm) is used to find a minimum/maximum spanning tree of the graph (spanning tree, in which is the sum of its edges weights minimal/maximal). The algorithm was developed in 1930 by Czech mathematician Vojtěch Jarník, in 1957 it was rediscovered by American mathematician Robert Prim. And again in 1959 the algorithm was rediscovered by Dutch computer scientist Edsger Dijkstra.

Description

The algorithm traverses the graph starting at a random node and maintains a list of already discovered nodes with their distance from the already connected (processed) subgraph. In every step the procedure connects a node, which is in the least distance, discovers its neighbours or recalculates their distance, if they had been already discovered and a more favorable edge was found. When all the nodes are connected to the subgraph, the algorithm terminates.

Complexity analysis

The complexity of the Jarník-Prim algorithm is dependent on the implementation of the list. The list itself may be modified at most times, because every discovery of a new edge may add a new node to the list or change a weight of some already discovered node.

If we implement the list using a binary heap, which acts as a priority queue, than its each modification takes steps. Hence the complexity of the Jarník-Prim algorithm is .

Code

/**
 * Jarnik-Prim algorithm
 * Finds the minimal spanning tree of the given graph
 * @graph graph
 * @weight edge weights  
 * @return array of predecessors  
 */ 
node[] jarnikPrimAlgorithm(graph, weight)
    Queue q
    q.addAllVetices(graph.vertices) //add all vertices to the queue
    
    distances = new int[q.size()] //array of distances
    distances[0] = 0 //root
    for i in 1 -> distances.length - 1 do                                 
        distances[i] = +inf //all remaining vertices are in infinite distance
     
    predecessors = new node[q.size()] //array of predecessors
    predecessors[0] = null //the root does not have any predecessor
    
    while !queue.empty() do //while the queue is not empty
        u = queue.extractMin() //return a node in a minimal distance
        for node in descendants(u) do //for all descendants of u
            if queue.contains(node) AND weight(u, node) < d[node] //if we have found some improving path to the descendant
                then predecessors[node] = u //than u is his predecessor
                     d[node] = weight(u, node) //and set a new distance    
    
    return predecessors //return the array of predecessors

Sources

• KOLÁŘ, Josef. Teoretická informatika. 2. edition. Prague : Česká informatická společnost, 2004. 205 p. ISBN 80-900853-8-5.